എല്ലാം കണക്കാ!
അമേരിക്കന് ഐക്യനാടുകളില് കണക്കും സയന്സും പഠിപ്പിക്കുന്നതിന്റെയും പഠിക്കുന്നതിന്റെയും നിലവാരം ഉയര്ത്തണമെന്ന വാദം ഉയര്ന്നു വന്നതില്പിന്നെ, ഈ വിഷയങ്ങള് ഏറ്റവും മോശമായി പഠിപ്പിക്കുന്നത് വാഷിംഗ്ടണ് സംസ്ഥാനത്തിലാണെന്ന് പല വിദ്യാഭ്യാസ വിചക്ഷണരും അഭിപ്രായപ്പെട്ടിട്ടുണ്ട്. ഹൈസ്കൂള് വിദ്യാഭ്യാസം പൂര്ത്തിയാക്കിയ കുട്ടികള്ക്ക് ഗുണനവും ഹരണവും അനായാസം കൈകാര്യം ചെയ്യാന് കഴിയുന്നില്ല എന്നത് പലരേയും അത്ഭുതപ്പെടുത്തുന്ന സംഗതിയായിരിക്കുന്നു.
മിക്ക രാജ്യങ്ങളിലും ഗുണനം പഠിപ്പിക്കുന്നത് സ്റ്റാന്ഡേഡ് അല്ഗരിഥം എന്ന പേരിലറിയപ്പെടുന്ന ‘സാധാരണ രീതി’യിലാണ്. ഉദാഹരണമായി, 34 നെ 51 കൊണ്ടു ഗുണിക്കണമെങ്കില് താഴെപ്പറയുന്ന രീതിയിലാവും ഗുണനഫലം കണ്ടെത്തുക:

ചിത്രം: സ്റ്റാന്ഡേഡ് അല്ഗരിഥം
ഈ രീതിയാണല്ലോ നമ്മളില് പലരും പഠിച്ചിരിക്കുന്നത്. (ഇപ്പോള് ഈ രീതി വിട്ട് പുതിയ രീതികള് പരീക്ഷിച്ചു തുടങ്ങിയിട്ടുണ്ടോ എന്നറിയാത്തതിനാലാണ് പലരും എന്നു പറഞ്ഞത്. ബ്ലോഗെഴുത്തുകാരെപ്പോലെ ബ്ലോഗുവായനക്കാരും കാല, ദേശ, പ്രായ, വര്ഗ്ഗ, വൈവിധ്യം നില നിറുത്തുന്നവരായതിനാല് “നമ്മളില് പലരും” എന്നൊക്കെ സൂക്ഷിച്ചേ പ്രയോഗിക്കാവൂ എന്ന് ആര്ക്കാണറിയാത്തത്?)
സ്റ്റാന്ഡേഡ് അല്ഗരിഥത്തിനെ ഇങ്ങനെ ചുരുക്കി എഴുതാവുന്നതാണ്:

ചിത്രം: സ്റ്റാന്ഡേഡ് അല്ഗരിഥം
എന്നാല് കുട്ടികളില് കണക്കു പഠനത്തോടൊപ്പം ചിന്താശീലവും അന്വേഷണത്വരയും ഗണിതേതര വിഷയങ്ങളില് പ്രാഗല്ഭ്യവും വളര്ത്തിയെടുക്കുകയാണത്രേ ഇവിടുത്തെ കണക്കു പഠനം കൊണ്ട് ലക്ഷ്യമിടുന്നത്. അമേരിക്കയാണെന്നു കരുതി, ‘ഗണിതേതര വിഷയങ്ങളില് പ്രാഗല്ഭ്യം’ എന്നു കേള്ക്കുമ്പോള് വായനക്കാരുടെ ഭാവന അതിരുകടക്കരുതേ! കണക്കു പുസ്തകത്തില് ലോക പരിചയം എന്ന പേരില് ലോകരാജ്യങ്ങളുടെയും അമേരിക്കന് സംസ്ഥാനങ്ങളുടെയും മറ്റും മാപുകളും മറ്റും ഉള്പ്പെടുത്തിയിരിക്കുന്നു എന്ന നിര്ദ്ദോഷമായ കൃത്യത്തെയാണ് ഞാന് ഉദ്ദേശിച്ചത്.
ഈ പാഠ്യ രീതിയാണ് ഇപ്പോള് വിമര്ശിക്കപ്പെട്ടിരിക്കുന്നത്. കണക്കു പഠനം നേരാം വണ്ണം നടക്കുന്നില്ലെന്ന് മാത്രമല്ല, അതിലുപരി നേടിയെടുക്കാന് ലക്ഷ്യമിട്ടിരുന്ന മറ്റു പല ബൌദ്ധിക പ്രവര്ത്തനങ്ങള്ക്കും പുതിയ രീതി വിലങ്ങുതടിയാണെന്നാണ് കണ്ടെത്തല്.
ഇതിനൊരു മറുവശവുമുണ്ടെന്ന് മറക്കുന്നില്ല. ഇപ്പോഴത്തെ രീതിയുടെ വക്താക്കള് പറയുന്നത്, എഞ്ചുവടിയും ലോഗരിഥം റ്റേയ്ബിളുമെല്ലാം പഴങ്കഥയായെന്നാണ്. ഇന്നത്തെ ലോകത്തിന്റെ ശാസ്ത്രീയാന്വേഷണത്തില് പങ്കാളികളാവുവാന് ഇത്തരം സാധാരണ ജോലികള് കാല്കുലേയ്റ്ററിനു വിട്ടുകൊടുക്കണമെന്നും ചെറുതായിരിക്കുമ്പോള്ത്തന്നെ വലിയ കാര്യങ്ങള് ചെയ്യുവാന് കുട്ടികളെ പ്രാപ്തരാക്കണമെന്നുമാണ് അവരുടെ വാദം.
എന്നാല് യഥാര്ഥത്തില് സംഭവിക്കുന്നത് മറ്റൊന്നാണ്. ക്ലാസിലെ ബുദ്ധിമാന്മാരും ബുദ്ധിമതികളും തങ്ങള്ക്കുമുന്നില് തുറന്നുകിട്ടുന്ന അവസരം ക്രിയാത്മകമായി വിനിയോഗിച്ച്, പാഠ്യപദ്ധതി ആവിഷ്കാരം ചെയ്തവരുടെ സ്വപ്നത്തിലുള്ള കണക്കു പഠനവുമായി അനന്താവസരങ്ങളുടെ ആകാശനീലിമയിലേയ്ക്കു പറന്നകലുന്നു. ആവറേയ്ജില് താഴെയുള്ള ബഹുഭൂരിപക്ഷം, നാലും മൂന്നും ഏഴെന്നെണ്ണാനും ഗണനയന്ത്രങ്ങള്ക്കടിമപ്പെടുന്നു.
ഗുണനം അഭ്യസിപ്പിക്കാന് നമ്മളില് പലരും പഠിച്ച സാധാരണ രീതി മുകളില് കണ്ടല്ലോ. എന്നാല് വാഷിംഗ്ടണ് സംസ്ഥാനത്തില് കുട്ടികളെ ഗുണനം പഠിപ്പിക്കുന്നതെങ്ങനെ എന്ന് നോക്കാം:

ചിത്രം: വാഷിംഗ്ടണ് സംസ്ഥാനം
ചില സ്കൂളുകളില് റ്റേര്ക് നിര്ദ്ദേശപ്രകാരമുള്ള Investigations in Numbers, Data, and Space എന്ന പദ്ധതിപ്രകാരം ക്ലസ്റ്റര് പ്രോബ്ലം പോലെയാണ് ഗുണനം പഠിപ്പിക്കുന്നത്. ചോദ്യത്തെ എളുപ്പത്തില് ഉത്തരം കണ്ടുപിടിക്കാവുന്ന പല കൂട്ടങ്ങളായി തിരിക്കുന്നതാണ് ക്ലസ്റ്റര് രീതി. മുന് ഉദാഹരണം തന്നെയെടുക്കുക. 34 x 51 എന്നത്, എളുപ്പത്തില് കണ്ടുപിടിക്കാവുന്ന 51- ന്റെ ഗുണിതങ്ങളാക്കുകയാണ് വേണ്ടത്.

ചിത്രം: ക്ലസ്റ്റര് രീതി
ഗുണിക്കേണ്ട സംഖ്യകള് വലുതാവുന്തോറും, കുട്ടികള്ക്ക് ചിന്താശീലത്തിനും അന്വേഷണത്വരയ്ക്കും പുറമേ പാഠ്യേതര വിഷയങ്ങളില് പ്രാഗല്ഭ്യവും വരുന്നതെങ്ങനെയെന്ന് ഊഹിക്കാമല്ലോ!
മറ്റു ചില സ്കൂളുകള് പിന്തുടരുന്ന Everyday Mathematics പാഠ്യരൂപം പാര്ഷ്യല് പ്രോഡക്ട്സ് രീതി എന്നും ലാറ്റിസ് രീതി എന്നും പേരായ രീതികള് പിന്തുടരാന് നിര്ദ്ദേശിക്കുന്നു.
പാര്ഷ്യല് പ്രോഡക്ട്സ് രീതി നമുക്കു പരിചിതമായ സാധാരണ രീതിയുമായി വളരെ സാമ്യമുള്ളതാണ്. ഈ രീതിയില് സംഖ്യകളുടെ സ്ഥാനക്രമം കുട്ടികള്ക്ക് വ്യക്തമാക്കിക്കൊടുക്കുന്നുണ്ട്. ചിത്രം നോക്കുക. ഇവിടെയും സംഖ്യകള് വലുതാവുമ്പോഴുണ്ടാകുന്ന പ്രശ്നങ്ങളെക്കുറിച്ച് ചിന്തിക്കുക.

ചിത്രം: പാര്ഷ്യല് പ്രോഡക്ട്സ് രീതി
Everyday Mathematics നിഷ്കര്ഷിക്കുന്ന ലാറ്റിസ് രീതി വളരെ രസാവഹമാണ്. ഗുണിക്കേണ്ടുന്ന സംഖ്യകള് മുകളിലും വലതും ആകത്തക്ക വിധം ഒരു ഗ്രിഡ് ഉണ്ടാക്കുകയാണ് ആദ്യപടി. രണ്ടു അക്കങ്ങള് ചേര്ന്നു വരുന്നയിടം രണ്ടായി പകുത്ത് (ചിത്രം കാണുക) അവിടെ രണ്ടു പകുതിയിലും കൂടി ആ സംഖ്യകളുടെ ഗുണനഫലം എഴുതിവയ്ക്കുക. ഗുണനഫലം ഒരക്ക സംഖ്യയാണെങ്കില് ഗുണനഫലത്തിന്റെ ആദ്യ അക്കമായി 0 ഉപയോഗിക്കാം. ഇങ്ങനെ ഓരോ അക്കങ്ങളുടെ ഗുണനഫലവും അതാതു ഗ്രിഡുകളില് എഴുതുക. ഇങ്ങനെ ചെയ്ത ശേഷം, ഡയഗണല് ആയി വരുന്ന അക്കങ്ങളുടെ തുക കണ്ടു പിടിക്കുക. ഇതില് നിന്നും സംഖ്യകളുടെ ഗുണനഫലത്തിലെത്തുന്ന വിധം താഴെ കാണിച്ചിരുക്കുന്നു.

ചിത്രം: ലാറ്റിസ് രീതി
കണക്കു പരീക്ഷയില് രണ്ടു സംഖ്യകളുടെ ഗുണനഫലം കാണേണ്ടിവരുമ്പോള് ലാറ്റിസ് രീതി മാത്രമറിയുന്നവര് സമയം പോകുന്നത് അറിയുകയേയില്ല.
ഇങ്ങനെയാണെങ്കിലും എനിക്ക് വളരെ പ്രിയങ്കരമായ പെസന്റ് രീതി സ്കൂളുകളില് പഠിപ്പിക്കുന്നതായി കാണുന്നില്ല. ആദ്യ വരിയില് ഗുണിക്കപ്പെടേണ്ട രണ്ടു സംഖ്യകള് നിരത്തിയെഴുതുക. രണ്ടാം വരിയില്, ആദ്യ സംഖ്യയുടെ താഴെ ആദ്യ സംഖ്യയെ രണ്ടു കൊണ്ട് ഹരിച്ച ഫലം (ശിഷ്ടം ഉപേക്ഷിക്കാം) എഴുതുക. രണ്ടാം സംഖ്യയ്ക്കു താഴെ, രണ്ടാം സംഖ്യയുടെ ഇരട്ടി എഴുതുക. വരിയിലെ ആദ്യസംഖ്യ ഒന്ന് ആകുന്നതു വരെ ഈ പ്രക്രിയ തുടരുക. ഇനി, ഓരോ വരിയിലെയും ആദ്യ സംഖ്യ നോക്കുക. ഈ സംഖ്യ ഇരട്ട സംഖ്യയാണെങ്കില് ആ വരിയിലെ രണ്ടാം സംഖ്യ വെട്ടിക്കളയുക. ഇങ്ങനെ ആദ്യ കോളത്തിലെ ഇരട്ടസംഖ്യകള്ക്കു നേരേ രണ്ടാം കോളത്തിലെഴുതിയിരിക്കുന്ന സംഖ്യകള് വെട്ടി മാറ്റിയ ശേഷം, രണ്ടാം കോളത്തില് ബാക്കിയാവുന്ന സംഖ്യകളുടെ തുകയായിരിക്കും ആ സംഖ്യകളുടെ ഗുണനഫലം.
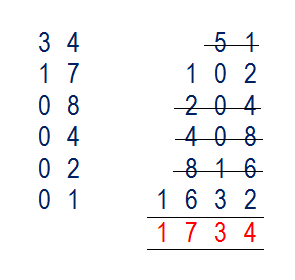
ചിത്രം: പെസന്റ് രീതി
ഗുണനവും ഹരണവുമെല്ലാം പഠിക്കുന്നതിനൊപ്പം കുട്ടികളുടെ ശാസ്ത്രാഭിവാഞ്ഛ വര്ധിപ്പിക്കുന്നത് നല്ലതാണെന്നതിന് ആര്ക്കും രണ്ടഭിപ്രായമില്ല. എന്നാല് പഠനം ലാറ്റിസ് രീതിയില് മാത്രമാവുകയും ദൈനംദിന ജീവിതത്തിലെ ചെറിയ കണക്കു കൂട്ടലുകള്ക്ക് ഈ രീതി അഭികാമ്യമല്ലാതാവുകയും ചെയ്യുമ്പോഴാണ് കുട്ടികള്ക്കൊപ്പം രക്ഷിതാക്കളും അഭിനവ പഠന രീതികളോട് പുറം തിരിഞ്ഞു നില്ക്കുന്നത്. സ്കൂളുകളില് സാധാരണ രീതി നിര്ബന്ധമായും പഠിപ്പിക്കണമെന്നും മറ്റു രീതികള് കൂടുതല് താല്പര്യമുള്ള വന്പുലികള് വിഹരിക്കേണ്ടുന്ന ഘോരവിപിനങ്ങളാക്കുന്നതില് തങ്ങള്ക്കെതിര്പ്പില്ലെന്നുമാണ് ഈ ‘മൂരാച്ചി’കളുടെ വാദം. അതില് കഴമ്പുണ്ടെന്ന് സമ്മതിക്കാതെ വയ്യ.
മിക്ക രാജ്യങ്ങളിലും ഗുണനം പഠിപ്പിക്കുന്നത് സ്റ്റാന്ഡേഡ് അല്ഗരിഥം എന്ന പേരിലറിയപ്പെടുന്ന ‘സാധാരണ രീതി’യിലാണ്. ഉദാഹരണമായി, 34 നെ 51 കൊണ്ടു ഗുണിക്കണമെങ്കില് താഴെപ്പറയുന്ന രീതിയിലാവും ഗുണനഫലം കണ്ടെത്തുക:

ചിത്രം: സ്റ്റാന്ഡേഡ് അല്ഗരിഥം
ഈ രീതിയാണല്ലോ നമ്മളില് പലരും പഠിച്ചിരിക്കുന്നത്. (ഇപ്പോള് ഈ രീതി വിട്ട് പുതിയ രീതികള് പരീക്ഷിച്ചു തുടങ്ങിയിട്ടുണ്ടോ എന്നറിയാത്തതിനാലാണ് പലരും എന്നു പറഞ്ഞത്. ബ്ലോഗെഴുത്തുകാരെപ്പോലെ ബ്ലോഗുവായനക്കാരും കാല, ദേശ, പ്രായ, വര്ഗ്ഗ, വൈവിധ്യം നില നിറുത്തുന്നവരായതിനാല് “നമ്മളില് പലരും” എന്നൊക്കെ സൂക്ഷിച്ചേ പ്രയോഗിക്കാവൂ എന്ന് ആര്ക്കാണറിയാത്തത്?)
സ്റ്റാന്ഡേഡ് അല്ഗരിഥത്തിനെ ഇങ്ങനെ ചുരുക്കി എഴുതാവുന്നതാണ്:

ചിത്രം: സ്റ്റാന്ഡേഡ് അല്ഗരിഥം
എന്നാല് കുട്ടികളില് കണക്കു പഠനത്തോടൊപ്പം ചിന്താശീലവും അന്വേഷണത്വരയും ഗണിതേതര വിഷയങ്ങളില് പ്രാഗല്ഭ്യവും വളര്ത്തിയെടുക്കുകയാണത്രേ ഇവിടുത്തെ കണക്കു പഠനം കൊണ്ട് ലക്ഷ്യമിടുന്നത്. അമേരിക്കയാണെന്നു കരുതി, ‘ഗണിതേതര വിഷയങ്ങളില് പ്രാഗല്ഭ്യം’ എന്നു കേള്ക്കുമ്പോള് വായനക്കാരുടെ ഭാവന അതിരുകടക്കരുതേ! കണക്കു പുസ്തകത്തില് ലോക പരിചയം എന്ന പേരില് ലോകരാജ്യങ്ങളുടെയും അമേരിക്കന് സംസ്ഥാനങ്ങളുടെയും മറ്റും മാപുകളും മറ്റും ഉള്പ്പെടുത്തിയിരിക്കുന്നു എന്ന നിര്ദ്ദോഷമായ കൃത്യത്തെയാണ് ഞാന് ഉദ്ദേശിച്ചത്.
ഈ പാഠ്യ രീതിയാണ് ഇപ്പോള് വിമര്ശിക്കപ്പെട്ടിരിക്കുന്നത്. കണക്കു പഠനം നേരാം വണ്ണം നടക്കുന്നില്ലെന്ന് മാത്രമല്ല, അതിലുപരി നേടിയെടുക്കാന് ലക്ഷ്യമിട്ടിരുന്ന മറ്റു പല ബൌദ്ധിക പ്രവര്ത്തനങ്ങള്ക്കും പുതിയ രീതി വിലങ്ങുതടിയാണെന്നാണ് കണ്ടെത്തല്.
ഇതിനൊരു മറുവശവുമുണ്ടെന്ന് മറക്കുന്നില്ല. ഇപ്പോഴത്തെ രീതിയുടെ വക്താക്കള് പറയുന്നത്, എഞ്ചുവടിയും ലോഗരിഥം റ്റേയ്ബിളുമെല്ലാം പഴങ്കഥയായെന്നാണ്. ഇന്നത്തെ ലോകത്തിന്റെ ശാസ്ത്രീയാന്വേഷണത്തില് പങ്കാളികളാവുവാന് ഇത്തരം സാധാരണ ജോലികള് കാല്കുലേയ്റ്ററിനു വിട്ടുകൊടുക്കണമെന്നും ചെറുതായിരിക്കുമ്പോള്ത്തന്നെ വലിയ കാര്യങ്ങള് ചെയ്യുവാന് കുട്ടികളെ പ്രാപ്തരാക്കണമെന്നുമാണ് അവരുടെ വാദം.
എന്നാല് യഥാര്ഥത്തില് സംഭവിക്കുന്നത് മറ്റൊന്നാണ്. ക്ലാസിലെ ബുദ്ധിമാന്മാരും ബുദ്ധിമതികളും തങ്ങള്ക്കുമുന്നില് തുറന്നുകിട്ടുന്ന അവസരം ക്രിയാത്മകമായി വിനിയോഗിച്ച്, പാഠ്യപദ്ധതി ആവിഷ്കാരം ചെയ്തവരുടെ സ്വപ്നത്തിലുള്ള കണക്കു പഠനവുമായി അനന്താവസരങ്ങളുടെ ആകാശനീലിമയിലേയ്ക്കു പറന്നകലുന്നു. ആവറേയ്ജില് താഴെയുള്ള ബഹുഭൂരിപക്ഷം, നാലും മൂന്നും ഏഴെന്നെണ്ണാനും ഗണനയന്ത്രങ്ങള്ക്കടിമപ്പെടുന്നു.
ഗുണനം അഭ്യസിപ്പിക്കാന് നമ്മളില് പലരും പഠിച്ച സാധാരണ രീതി മുകളില് കണ്ടല്ലോ. എന്നാല് വാഷിംഗ്ടണ് സംസ്ഥാനത്തില് കുട്ടികളെ ഗുണനം പഠിപ്പിക്കുന്നതെങ്ങനെ എന്ന് നോക്കാം:

ചിത്രം: വാഷിംഗ്ടണ് സംസ്ഥാനം
ചില സ്കൂളുകളില് റ്റേര്ക് നിര്ദ്ദേശപ്രകാരമുള്ള Investigations in Numbers, Data, and Space എന്ന പദ്ധതിപ്രകാരം ക്ലസ്റ്റര് പ്രോബ്ലം പോലെയാണ് ഗുണനം പഠിപ്പിക്കുന്നത്. ചോദ്യത്തെ എളുപ്പത്തില് ഉത്തരം കണ്ടുപിടിക്കാവുന്ന പല കൂട്ടങ്ങളായി തിരിക്കുന്നതാണ് ക്ലസ്റ്റര് രീതി. മുന് ഉദാഹരണം തന്നെയെടുക്കുക. 34 x 51 എന്നത്, എളുപ്പത്തില് കണ്ടുപിടിക്കാവുന്ന 51- ന്റെ ഗുണിതങ്ങളാക്കുകയാണ് വേണ്ടത്.

ചിത്രം: ക്ലസ്റ്റര് രീതി
ഗുണിക്കേണ്ട സംഖ്യകള് വലുതാവുന്തോറും, കുട്ടികള്ക്ക് ചിന്താശീലത്തിനും അന്വേഷണത്വരയ്ക്കും പുറമേ പാഠ്യേതര വിഷയങ്ങളില് പ്രാഗല്ഭ്യവും വരുന്നതെങ്ങനെയെന്ന് ഊഹിക്കാമല്ലോ!
മറ്റു ചില സ്കൂളുകള് പിന്തുടരുന്ന Everyday Mathematics പാഠ്യരൂപം പാര്ഷ്യല് പ്രോഡക്ട്സ് രീതി എന്നും ലാറ്റിസ് രീതി എന്നും പേരായ രീതികള് പിന്തുടരാന് നിര്ദ്ദേശിക്കുന്നു.
പാര്ഷ്യല് പ്രോഡക്ട്സ് രീതി നമുക്കു പരിചിതമായ സാധാരണ രീതിയുമായി വളരെ സാമ്യമുള്ളതാണ്. ഈ രീതിയില് സംഖ്യകളുടെ സ്ഥാനക്രമം കുട്ടികള്ക്ക് വ്യക്തമാക്കിക്കൊടുക്കുന്നുണ്ട്. ചിത്രം നോക്കുക. ഇവിടെയും സംഖ്യകള് വലുതാവുമ്പോഴുണ്ടാകുന്ന പ്രശ്നങ്ങളെക്കുറിച്ച് ചിന്തിക്കുക.

ചിത്രം: പാര്ഷ്യല് പ്രോഡക്ട്സ് രീതി
Everyday Mathematics നിഷ്കര്ഷിക്കുന്ന ലാറ്റിസ് രീതി വളരെ രസാവഹമാണ്. ഗുണിക്കേണ്ടുന്ന സംഖ്യകള് മുകളിലും വലതും ആകത്തക്ക വിധം ഒരു ഗ്രിഡ് ഉണ്ടാക്കുകയാണ് ആദ്യപടി. രണ്ടു അക്കങ്ങള് ചേര്ന്നു വരുന്നയിടം രണ്ടായി പകുത്ത് (ചിത്രം കാണുക) അവിടെ രണ്ടു പകുതിയിലും കൂടി ആ സംഖ്യകളുടെ ഗുണനഫലം എഴുതിവയ്ക്കുക. ഗുണനഫലം ഒരക്ക സംഖ്യയാണെങ്കില് ഗുണനഫലത്തിന്റെ ആദ്യ അക്കമായി 0 ഉപയോഗിക്കാം. ഇങ്ങനെ ഓരോ അക്കങ്ങളുടെ ഗുണനഫലവും അതാതു ഗ്രിഡുകളില് എഴുതുക. ഇങ്ങനെ ചെയ്ത ശേഷം, ഡയഗണല് ആയി വരുന്ന അക്കങ്ങളുടെ തുക കണ്ടു പിടിക്കുക. ഇതില് നിന്നും സംഖ്യകളുടെ ഗുണനഫലത്തിലെത്തുന്ന വിധം താഴെ കാണിച്ചിരുക്കുന്നു.

ചിത്രം: ലാറ്റിസ് രീതി
കണക്കു പരീക്ഷയില് രണ്ടു സംഖ്യകളുടെ ഗുണനഫലം കാണേണ്ടിവരുമ്പോള് ലാറ്റിസ് രീതി മാത്രമറിയുന്നവര് സമയം പോകുന്നത് അറിയുകയേയില്ല.
ഇങ്ങനെയാണെങ്കിലും എനിക്ക് വളരെ പ്രിയങ്കരമായ പെസന്റ് രീതി സ്കൂളുകളില് പഠിപ്പിക്കുന്നതായി കാണുന്നില്ല. ആദ്യ വരിയില് ഗുണിക്കപ്പെടേണ്ട രണ്ടു സംഖ്യകള് നിരത്തിയെഴുതുക. രണ്ടാം വരിയില്, ആദ്യ സംഖ്യയുടെ താഴെ ആദ്യ സംഖ്യയെ രണ്ടു കൊണ്ട് ഹരിച്ച ഫലം (ശിഷ്ടം ഉപേക്ഷിക്കാം) എഴുതുക. രണ്ടാം സംഖ്യയ്ക്കു താഴെ, രണ്ടാം സംഖ്യയുടെ ഇരട്ടി എഴുതുക. വരിയിലെ ആദ്യസംഖ്യ ഒന്ന് ആകുന്നതു വരെ ഈ പ്രക്രിയ തുടരുക. ഇനി, ഓരോ വരിയിലെയും ആദ്യ സംഖ്യ നോക്കുക. ഈ സംഖ്യ ഇരട്ട സംഖ്യയാണെങ്കില് ആ വരിയിലെ രണ്ടാം സംഖ്യ വെട്ടിക്കളയുക. ഇങ്ങനെ ആദ്യ കോളത്തിലെ ഇരട്ടസംഖ്യകള്ക്കു നേരേ രണ്ടാം കോളത്തിലെഴുതിയിരിക്കുന്ന സംഖ്യകള് വെട്ടി മാറ്റിയ ശേഷം, രണ്ടാം കോളത്തില് ബാക്കിയാവുന്ന സംഖ്യകളുടെ തുകയായിരിക്കും ആ സംഖ്യകളുടെ ഗുണനഫലം.

ചിത്രം: പെസന്റ് രീതി
ഗുണനവും ഹരണവുമെല്ലാം പഠിക്കുന്നതിനൊപ്പം കുട്ടികളുടെ ശാസ്ത്രാഭിവാഞ്ഛ വര്ധിപ്പിക്കുന്നത് നല്ലതാണെന്നതിന് ആര്ക്കും രണ്ടഭിപ്രായമില്ല. എന്നാല് പഠനം ലാറ്റിസ് രീതിയില് മാത്രമാവുകയും ദൈനംദിന ജീവിതത്തിലെ ചെറിയ കണക്കു കൂട്ടലുകള്ക്ക് ഈ രീതി അഭികാമ്യമല്ലാതാവുകയും ചെയ്യുമ്പോഴാണ് കുട്ടികള്ക്കൊപ്പം രക്ഷിതാക്കളും അഭിനവ പഠന രീതികളോട് പുറം തിരിഞ്ഞു നില്ക്കുന്നത്. സ്കൂളുകളില് സാധാരണ രീതി നിര്ബന്ധമായും പഠിപ്പിക്കണമെന്നും മറ്റു രീതികള് കൂടുതല് താല്പര്യമുള്ള വന്പുലികള് വിഹരിക്കേണ്ടുന്ന ഘോരവിപിനങ്ങളാക്കുന്നതില് തങ്ങള്ക്കെതിര്പ്പില്ലെന്നുമാണ് ഈ ‘മൂരാച്ചി’കളുടെ വാദം. അതില് കഴമ്പുണ്ടെന്ന് സമ്മതിക്കാതെ വയ്യ.
26 Comments:
ഫിന്നിഷ് കുട്ടികള് ആണത്ര ലോകത്തില് ഏറ്റവും മിടുക്കന്മാര് കണക്കില് . അവര് എന്താണ് ചെയ്യുന്നേ എങ്ങിനെയാണ് പഠിപ്പിക്കുന്നെ എന്നാര്ക്കെങ്കിലും അറിയാമെങ്കില് ഈ പഠനമുറകളുമായി ഒരു കമ്പാരിസണ് നടത്താമായിരുന്നു.
മാതിലും സയന്സിലും ഏഷ്യന് രാജ്യങ്ങള് മുന്നിലാണെന്ന് ഈ സ്റ്റഡി പറയുന്നു.
:)
സന്തോഷേട്ടാ ദേ ഇത് ഒന്ന് കണ്ട് നോക്ക്യേ.
QW_ER_TY
നല്ല ലേഖനം സന്തോഷ്ജീ :-))
ഫിന്നിഷ് ആണോ കണ്ക്കില് മിടുക്കര്? ഇന്ത്യന് പട്ടന്മാരാണെന്നാ ഞാന് കരുതിയേ :-)
(എന്നോട് ഒരു ഇന്റര്വ്യൂവില് ചോദിച്ച ചോദ്യം :
ആന് ഓറഞ്ച് കോസ്റ്റ്സ് 18 ഡോളേര്സ്
എ പൈനാപ്പിള് കോസ്റ്റ്സ് 27 ഡോളേര്സ്
എ ഗ്രേപ്പ് കോസ്റ്റ്സ് 15 ഡോളേര്സ്...
സോ ഹൌ മച്ച് ഡസ് എ മാംഗോ കോസ്റ്റ്?”
ഞാന് സോള്വ് ചെയ്ത ഏറ്റം പ്രയാസമേറിയ കണക്കും അതന്നെ. :-(
ഡോളേര്സ് അല്ലാ ട്ടാ...സെന്റ്സ്.....
;-)
സന്തോഷിന്റെ കുറിപ്പുകള് വായിച്ചാല് എന്തെങ്കിലും പുതിയത് കിട്ടും.
സംശയം : കണക്ക് + ഇതര = കണക്കിതര എന്നു വരണമെന്നും കണക്കേതര ആവരുതെന്നുമല്ലേ ഉമേഷ് പറഞ്ഞത്? അതോ തിരിച്ചാണോ?
കണക്ക് പാഠത്തില് കണക്കിതര സംശയം ചോദിച്ചതിന് ഓമന (ഓമന = ഓഫിന് മാപ്പ് നല്കൂ കട: അരവിന്ദ്)
പെസന്റ് രീതി ഇതു വരെ അറിയാത്ത ഒന്നായിരുന്നു സന്തോഷേ.
ക്ലസ്റ്റര് രീതി വേദിക് മാത്തമാറ്റിക്സിന്റേതായി കുറേ കുട്ടികളെ പഠിപ്പിച്ചിട്ടുണ്ടു്. രണ്ടക്കത്തില് കൂടിയാല് 50 ശതമാനം പേരും തെറ്റിക്കുന്നതായാണു് കണ്ടു വന്നിട്ടുള്ളതു്. അക്കത്തില് വ്യത്യാസം വന്നാല്, അതായതു് മൂന്നക്ക സംഖ്യയും നാലക്ക സംഖ്യയും തമ്മില് പെരുക്കുന്നതാണെങ്കില് 90 ശതമാനവും തെറ്റായിരിക്കും. ഇതൊക്കെ പക്ഷേ ചെറിയ ക്ലാസ്സു മുതല്ക്കേ തുടങ്ങിയിരുന്നെങ്കില് ഇങ്ങനെ തെറ്റില്ലായിരുന്നുവെന്നും അഞ്ചക്കം വരെ പത്താംക്ലാസ്സുകാരനു് മനസ്സില് ചെയ്യാന് കഴിയുമെന്നും തോന്നുന്നു.
പറയാന് വന്നതൊരു ഓഫാണു്. പഠിച്ചതു് ഇംഗ്ലീഷ് മീഡിയത്തിലായിരുന്നിട്ടും എനിക്കിപ്പൊഴും ഏഴേഴു നാല്പ്പത്തൊന്പതു്, ഒമ്പയ്റ്റഞ്ചു് നാല്പ്പത്തഞ്ചു് എന്നൊക്കെ ചൊല്ലിയാലേ കിട്ടൂ. വ്യവഹാരത്തിലുള്ള ഭാഷയില് വേണം പഠിക്കാന് എന്നാര്ക്കെങ്കിലും അഭിപ്രായമുണ്ടോ?
എങ്ങനെ പഠിപ്പിക്കണം എന്നു് നമ്മുടെ നാട്ടിലാരെങ്കിലും ചിന്തിക്കുന്നുണ്ടോ ആവോ!
സന്തോഷ്ജി,
നല്ല ലേഖനം. വളരെ നന്ദി. കണ്ണൂസ്ജി പറഞതു കേട്ടല്ലോ? ഗണിതേതരം/കണക്കിതരം (എല്ലാം കണക്കാ:-)
പെരുക്കപ്പട്ടിക, മൂന്നുമുതല് അഞ്ചുവരെ വയസ്സുള്ളപ്പോള് പഠിപ്പിക്കാന് തുടങിയാല് അതു വളരെ നല്ല കാര്യമായിരിയ്ക്കും. അര്ഥം, ആവശ്യം എന്നതൊന്നും അറിയില്ലെങ്കിലും, എന്തെങ്കിലുമൊക്കെ വായില്ത്തോന്നിയത് പാടിനടക്കുന്നകാലമല്ലേ. കിട്ടുന്നതെന്തും മൂളി, പാടി, വായിട്ടലച്ച്... അങനെ പഠിയ്ക്കാന് തുടങും കുറേശ്ശെയായി...
മനഃപ്പാഠം പഠിയ്ക്കാന് ഏറ്റവും നല്ല സമയം നന്നായി ഉപയോഗപ്പെടുത്താമല്ലോ. പക്ഷേ, പിന്നീട്, വലുതാവുന്നതനുസരിച്ച്, പഠിച്ചകാര്യങളുടെയെല്ലാം പൊരുള് തേടാനുള്ള ആഗ്രഹവും സൌകര്യവും സ്വാതന്ത്ര്യവും ഉണ്ടായാല് വളരെ നന്നായി.
ഈ പോസ്റ്റിനു നന്ദി.
കുഴപ്പമായല്ലോ റ്റീച്ചറേ. കണക്കിതരം കണക്കാണോ? അപ്പോള് കണക്കേതരമാണോ ശരി?
ദൈവമെ .. കണക്കുചെയ്യാന് ഇത്രയും മെതേഡ്സോ.. കണ്ടു കണ്ണു തള്ളിപ്പോയി.. എനിക്കാകെ ഒരു രീതിയെ അറിയൂ.. അത് ആ കമലാക്ഷി ടീച്ചര് പഠിപ്പിച്ചതാ..അതും കൊണ്ടാ ഇവിടെ വരെ എത്തിയേ.. (കഷ്ടം ..) ഇതില് പറഞ്ഞതു വെച്ച് സാധാരണ രീതി.. ഇതു കൊള്ളാം .. ഒന്നു പരീക്ഷിച്ചു നോക്കട്ടെ..
ഇതിന്റെയൊക്കെ വല്ല ആവശ്യവുമുണ്ടോ സായിപ്പന്മാര്ക്ക്...നാട്ടിലെ രീതി അവര് കണ്ടിട്ടില്ലാ അതാ.
ഒരു വള്ളിച്ചൂരല്....അല്ലെങ്കില് റൂള് തടി......പിള്ളേര് മുള്ളിക്കൊണ്ട് 'ലോഹരിതം' പഠിക്കും.
‘കണക്കായിപ്പോയി‘ എന്നു പറയുന്നത് ഇതിനെ ആണോ ?
(ഓടോ: സന്തോഷേ, നല്ല പോസ്റ്റ്.
കണ്ടപ്പോള് ഓഫ് അടിക്കാനാ തോന്നിയെ.പെസന്റ് രീതി കൊള്ളാം. പുതിയ അറിവ്.)
നല്ല ലേഖനം…
കുട്ടികളെ പണ്ടത്തെ രീതിയില്ഗു ണനപട്ടിക ചെറുപ്പത്തിലേ പഠിപ്പിയ്ക്കുന്ന രീതി നല്ലതാണെന്നാണ് എനിയ്ക്ക് തോന്നുന്നത്.
കണക്ക് റ്റീച്ചറാണെങ്കിലും ഈ പെസന്റ് രീതി ഞാനാദ്യായിട്ടാന് കാണുന്നതു.അതെനിയ്ക്കിഷ്ടപ്പെട്ടു.കൂടാതെ ബിരിയാണിക്കുട്ടിടെ ലിങ്കും.
:)
സ്റ്റാന്ഡേര്ഡ് അല്ഗരിതത്തിന്റെ ഗ്രാഫിക് റെപ്രസെന്റേഷന് ആണു ബിക്കു തന്ന ലിങ്ക്. തത്ത്വം ഇങ്ങനെ തന്നെ പഠിപ്പിക്കുന്നതു നല്ലതാണു്. പക്ഷേ ഗുണിക്കാന് ആ വശ്ഴി ഉപയോഗിക്കരുതു്.
രണ്ടാം ക്ലാസുകാരനായ ആജുവിനെ ഞാനിപ്പോള് എങ്ങനെ രണ്ട് കൊണ്ടുള്ള ഗുണനം പഠിപ്പിക്കും?
നല്ല ലേഖനം സന്തോഷ്.മുറം പോലുള്ള പുസ്തകം വരുന്നതിന്റെ മുമ്പ് കണക്ക് പുസ്തകത്തിലെ അഭ്യാസങ്ങള് a,b,c എന്ന മൂന്ന് ഗ്രേഡിലായിരുന്നു കൊടുത്തിരുന്നത്.
സന്തോഷേട്ടാ,
ദേ ഇത് ബിബീസിന്റെ ലിങ്കാണ്.
http://news.bbc.co.uk/2/hi/uk_news/education/4073753.stm
സന്തോഷേട്ടന്റെ ലിങ്കില് (അതു മിഷിഗണ് കേന്ദ്രീകരിച്ചിരിക്കുന്നതല്ലേ?) ചെറിയൊരു ടേമ്പിളേ അവര് കാണിക്കുന്നുള്ളൂ.
കണ്സിക്ക്യൂട്ടിവായി ഫിന്ലാണ്ടാണ് മുന്നില്. ലിങ്കൊന്നും ഇപ്പൊ ഇല്ല്ല്ല.എപ്പോഴൊക്കെയൊ വായിച്ചതാണ്. ഹോങ്ങ് കോങ്ങിലുള്ളത് ബ്രിട്ടീഷ് സിസ്റ്റമായിരിക്കില്ലെ? ഏഷ്യന് സിസ്റ്റമായിരിക്കുമൊ?
ഇതില് ഒക്കെ ഇന്ത്യ എവിടെ? ടുണീഷ്യ ഇന്തോനേഷ്യയെ കുറിച്ചൊക്കെ വന്നു. നമ്മള് എവിടെ? നമ്മളെ കണക്ക് പഠിപ്പിക്കുന്ന സിസ്റ്റം പഴയ ബ്രിട്ടീഷ് സിസ്റ്റമാണൊ?
എനിക്ക് സത്യത്തില് ഇവിടുത്തെ കണക്കു പഠിപ്പിക്കുന്ന രീതി ഓര്ത്തിട്ട് പേടി ആണ്. ഞാന് മോളെ നമ്മളൊക്കെ പഠിച്ച രീതിയില് പഠിപ്പിച്ചു, ഒരു ദിവസം അവള് വന്നു പറഞ്ഞു ടീച്ചര് ഇങ്ങനെ അല്ല പറഞ്ഞു തന്നത് എന്ന്.ഇനി അവള് ക്ലാസ്സില് പഠിക്കട്ടെ, രണ്ടും കൂടി ആയി ഒന്നും ഇല്ലാതെ ആവണ്ടല്ലൊ. എന്നാലും എനിക്ക് ...
അഭിപ്രായങ്ങള്ക്കു നന്ദി. ഛെ, മുഴുവന് തെറ്റുകളാണല്ലോ. കണക്കേതരം അറിവില്ലായ്മയാണ്(ഓര്മ്മക്കുറവും. ഉമേഷിന്റെ ലേഖനം ഞാന്ന് വായിച്ചതാണ്, സത്യം!). വിചക്ഷണര് തെറ്റിയത് സഹിക്കാനാവുന്നില്ല. എല്ലാം തിരുത്തുന്നു.
ബിക്കുവിന്റെ ലിങ്ക് ലാറ്റിസ് മെതേഡിന്റെയും അടിസ്ഥാനം തന്നെ.
എന്തരോ എന്തോ..? കാല്കക്കുലേറ്റര് ഇല്ലാതെയും കണക്കു് കൂട്ടാന് അറിയാവുന്നവരുണ്ടാകട്ടേ..!
എന്റമ്മേ, ഈ ഗുണിക്കുന്ന രീതിയെല്ലാം കണ്ടിട്ടു കണ്ണു തള്ളി :(
സ്റ്റാന്ഡേഡ് അല്ഗരിഥം രീതിയില് അല്ലേ ഏറ്റവും കുറവു തെറ്റ് വരാന് സാധ്യത?( കാരണം എഴുതുന്ന അക്കങ്ങള് ഏറ്റവും കുറവ്) ബാക്കി രീതികളില് പോയാല് എഴുതുന്നതിന്റെ ഇടയില് ഒരക്കം തെറ്റിയാം മൊത്തം പോയില്ലേ? ഇനി പേപ്പറില് എഴുതി കണക്കു പഠിപ്പിക്കുന്ന രീതി അമേരിക്കയില് ഇല്ലേ?
കുട്ടികള് കാല്കുലേറ്റര് ഉപയോഗിച്ചാല് അവരുടെ ബുദ്ധിശക്തി വികസിക്കുവാനുള്ള അവസരം കുറയുകലല്ലേ ചെയ്യുക, കൂടുതല് മഷീന് അധിഷ്ഠിതമായൊരു തലമുറ സൃഷ്ടിക്കുകയല്ലേ ചെയ്യുന്നത്?
ഈ ലേഖനത്തിനു പ്രത്യേകം നന്ദി.. പണ്ട് ബി.എസ്.സി (മാത്തമാറ്റിക്സ്)നു ഡിസ്റ്റിങ്ങ്ഷന് വാങ്ങി തുള്ളിച്ചാടി ചെന്നപ്പോല് "കണക്ക പിള്ളെ ദാ ഈ കിടക്കുന്ന പ്ളാവിണ്റ്റെ തടിക്കഷണം എത്ര കണ്ടി യുണ്ട്., തൊലിക്കനം കളഞ്ഞിട്ടു....ഒന്നു പറഞ്ഞെ "എന്നു മുത്തശ്ശന് ചോദിച്ചതും കണ്ണുമിഴിച്ച എന്നെ അപ്ളൈഡ് മാത്ത് കൊഞ്ഞനം കുത്തിയതും...
നല്ല ലേഖനം
ഹരിച്ചും ഗുണിച്ചും നോക്കുമ്പോള് ഉത്തരം ശരിയാണെന്ന് തോന്നിയാലും ഒന്നുകൂടി ഹരിച്ചും ഗുണിച്ചും നോക്കുന്നത് നല്ലതാണെന്ന് മണിച്ചിത്രത്താഴില് ഡോ.സണ്ണി പറഞ്ഞതു ഓര്ത്തുപോയി.
ഇവിടെ കുട്ടികളുടെ കണക്കുപഠിത്തം ഈ വഴിക്കാണെന്ന് പറഞ്ഞുതന്നതിനു നന്ദി സന്തോഷ്!
കണക്കെനിക്ക് ഒരു കണക്കായതുകൊണ്ട്, ഈ കമന്റ് കണക്കാക്കേണ്ട.
പക്ഷെ, പല കാര്യങ്ങളും ഇത് വായിച്ച് അറിയാന് കഴിഞ്ഞു.
സത്യത്തില് എനിക്ക് ലാറ്റിസ് രീതി വളരെ ഇഷ്ടപ്പെട്ടു. കണക്കില് തെറ്റുവരുത്തല് പതിവുള്ള എനിക്ക് അത് വളരെ സഹായമായേനേ. ഗുണിച്ചുകൊണ്ടിരിക്കുമ്പോള് കൂട്ടല് വേണ്ട, കൂട്ടിക്കൊണ്ടിരിക്കുമ്പോള് ഗുണനവും വേണ്ട എന്നതാണ് അതില് പിഴവ് കുറവാവും എന്ന് ഞാന് പറഞ്ഞതിന്റെ കാരണം. പിന്നെ, ഇത്ര വലിയ ഗ്രിഡ് ഒന്നും വരയ്ക്കേണ്ട. ഒരു വലിയ സ്ക്വയറും അതിനുള്ളില് ഡയഗണല് ലൈന്സും മാത്രം മതി.
Post a Comment
<< Home