എല്ലാം കണക്കാ!

അമേരിക്കന്‍ ഐക്യനാടുകളില്‍ കണക്കും സയന്‍സും പഠിപ്പിക്കുന്നതിന്‍റെയും പഠിക്കുന്നതിന്‍റെയും നിലവാരം ഉയര്‍ത്തണമെന്ന വാദം ഉയര്‍ന്നു വന്നതില്‍പിന്നെ, ഈ വിഷയങ്ങള്‍ ഏറ്റവും മോശമായി പഠിപ്പിക്കുന്നത് വാഷിംഗ്ടണ്‍ സംസ്ഥാനത്തിലാണെന്ന് പല വിദ്യാഭ്യാസ വിചക്ഷണരും അഭിപ്രായപ്പെട്ടിട്ടുണ്ട്. ഹൈസ്കൂള്‍ വിദ്യാഭ്യാസം പൂര്‍ത്തിയാക്കിയ കുട്ടികള്‍ക്ക് ഗുണനവും ഹരണവും അനായാസം കൈകാര്യം ചെയ്യാന്‍ കഴിയുന്നില്ല എന്നത് പലരേയും അത്ഭുതപ്പെടുത്തുന്ന സംഗതിയായിരിക്കുന്നു.

മിക്ക രാജ്യങ്ങളിലും ഗുണനം പഠിപ്പിക്കുന്നത് സ്റ്റാന്‍ഡേഡ് അല്‍ഗരിഥം എന്ന പേരിലറിയപ്പെടുന്ന ‘സാധാരണ രീതി’യിലാണ്. ഉദാഹരണമായി, 34 നെ 51 കൊണ്ടു ഗുണിക്കണമെങ്കില്‍ താഴെപ്പറയുന്ന രീതിയിലാവും ഗുണനഫലം കണ്ടെത്തുക:


ചിത്രം: സ്റ്റാന്‍‍ഡേഡ് അല്‍ഗരിഥം

ഈ രീതിയാണല്ലോ നമ്മളില്‍ പലരും പഠിച്ചിരിക്കുന്നത്. (ഇപ്പോള്‍ ഈ രീതി വിട്ട് പുതിയ രീതികള്‍ പരീക്ഷിച്ചു തുടങ്ങിയിട്ടുണ്ടോ എന്നറിയാത്തതിനാലാണ് പലരും എന്നു പറഞ്ഞത്. ബ്ലോഗെഴുത്തുകാരെപ്പോലെ ബ്ലോഗുവായനക്കാരും കാല, ദേശ, പ്രായ, വര്‍ഗ്ഗ, വൈവിധ്യം നില നിറുത്തുന്നവരായതിനാല്‍ “നമ്മളില്‍ പലരും” എന്നൊക്കെ സൂക്ഷിച്ചേ പ്രയോഗിക്കാവൂ എന്ന് ആര്‍ക്കാണറിയാത്തത്?)

സ്റ്റാന്‍‍ഡേഡ് അല്‍ഗരിഥത്തിനെ ഇങ്ങനെ ചുരുക്കി എഴുതാവുന്നതാണ്:


ചിത്രം: സ്റ്റാന്‍‍ഡേഡ് അല്‍ഗരിഥം

എന്നാല്‍ കുട്ടികളില്‍ കണക്കു പഠനത്തോടൊപ്പം ചിന്താശീലവും അന്വേഷണത്വരയും ഗണിതേതര വിഷയങ്ങളില്‍ പ്രാഗല്ഭ്യവും വളര്‍ത്തിയെടുക്കുകയാണത്രേ ഇവിടുത്തെ കണക്കു പഠനം കൊണ്ട് ലക്ഷ്യമിടുന്നത്. അമേരിക്കയാണെന്നു കരുതി, ‘ഗണിതേതര വിഷയങ്ങളില്‍ പ്രാഗല്ഭ്യം’ എന്നു കേള്‍ക്കുമ്പോള്‍ വായനക്കാരുടെ ഭാവന അതിരുകടക്കരുതേ! കണക്കു പുസ്തകത്തില്‍ ലോക പരിചയം എന്ന പേരില്‍ ലോകരാജ്യങ്ങളുടെയും അമേരിക്കന്‍ സംസ്ഥാനങ്ങളുടെയും മറ്റും മാപുകളും മറ്റും ഉള്‍പ്പെടുത്തിയിരിക്കുന്നു എന്ന നിര്‍ദ്ദോഷമായ കൃത്യത്തെയാണ് ഞാന്‍ ഉദ്ദേശിച്ചത്.

ഈ പാഠ്യ രീതിയാണ് ഇപ്പോള്‍ വിമര്‍ശിക്കപ്പെട്ടിരിക്കുന്നത്. കണക്കു പഠനം നേരാം വണ്ണം നടക്കുന്നില്ലെന്ന് മാത്രമല്ല, അതിലുപരി നേടിയെടുക്കാന്‍ ലക്ഷ്യമിട്ടിരുന്ന മറ്റു പല ബൌദ്ധിക പ്രവര്‍ത്തനങ്ങള്‍ക്കും പുതിയ രീതി വിലങ്ങുതടിയാണെന്നാണ് കണ്ടെത്തല്‍.

ഇതിനൊരു മറുവശവുമുണ്ടെന്ന് മറക്കുന്നില്ല. ഇപ്പോഴത്തെ രീതിയുടെ വക്താക്കള്‍ പറയുന്നത്, എഞ്ചുവടിയും ലോഗരിഥം റ്റേയ്ബിളുമെല്ലാം പഴങ്കഥയായെന്നാണ്. ഇന്നത്തെ ലോകത്തിന്‍റെ ശാസ്ത്രീയാന്വേഷണത്തില്‍ പങ്കാളികളാവുവാന്‍ ഇത്തരം സാധാരണ ജോലികള്‍ കാല്‍കുലേയ്റ്ററിനു വിട്ടുകൊടുക്കണമെന്നും ചെറുതായിരിക്കുമ്പോള്‍ത്തന്നെ വലിയ കാര്യങ്ങള്‍ ചെയ്യുവാന്‍ കുട്ടികളെ പ്രാപ്തരാക്കണമെന്നുമാണ് അവരുടെ വാദം.

എന്നാല്‍ യഥാര്‍ഥത്തില്‍ സംഭവിക്കുന്നത് മറ്റൊന്നാണ്. ക്ലാസിലെ ബുദ്ധിമാന്മാരും ബുദ്ധിമതികളും തങ്ങള്‍ക്കുമുന്നില്‍ തുറന്നുകിട്ടുന്ന അവസരം ക്രിയാത്മകമായി വിനിയോഗിച്ച്, പാഠ്യപദ്ധതി ആവിഷ്കാരം ചെയ്തവരുടെ സ്വപ്നത്തിലുള്ള കണക്കു പഠനവുമായി അനന്താവസരങ്ങളുടെ ആകാശനീലിമയിലേയ്ക്കു പറന്നകലുന്നു. ആവറേയ്ജില്‍ താഴെയുള്ള ബഹുഭൂരിപക്ഷം, നാലും മൂന്നും ഏഴെന്നെണ്ണാനും ഗണനയന്ത്രങ്ങള്‍ക്കടിമപ്പെടുന്നു.

ഗുണനം അഭ്യസിപ്പിക്കാന്‍ നമ്മളില്‍ പലരും പഠിച്ച സാധാരണ രീതി മുകളില്‍ കണ്ടല്ലോ. എന്നാല്‍ വാഷിംഗ്ടണ്‍ സംസ്ഥാനത്തില്‍ കുട്ടികളെ ഗുണനം പഠിപ്പിക്കുന്നതെങ്ങനെ എന്ന് നോക്കാം:


ചിത്രം: വാഷിംഗ്ടണ്‍ സംസ്ഥാനം

ചില സ്കൂളുകളില്‍ റ്റേര്‍ക് നിര്‍ദ്ദേശപ്രകാരമുള്ള Investigations in Numbers, Data, and Space എന്ന പദ്ധതിപ്രകാരം ക്ലസ്റ്റര്‍ പ്രോബ്ലം പോലെയാണ് ഗുണനം പഠിപ്പിക്കുന്നത്. ചോദ്യത്തെ എളുപ്പത്തില്‍ ഉത്തരം കണ്ടുപിടിക്കാവുന്ന പല കൂട്ടങ്ങളായി തിരിക്കുന്നതാണ് ക്ലസ്റ്റര്‍ രീതി. മുന്‍ ഉദാഹരണം തന്നെയെടുക്കുക. 34 x 51 എന്നത്, എളുപ്പത്തില്‍ കണ്ടുപിടിക്കാവുന്ന 51- ന്‍റെ ഗുണിതങ്ങളാക്കുകയാണ് വേണ്ടത്.


ചിത്രം: ക്ലസ്റ്റര്‍ രീതി

ഗുണിക്കേണ്ട സംഖ്യകള്‍ വലുതാവുന്തോറും, കുട്ടികള്‍ക്ക് ചിന്താശീലത്തിനും അന്വേഷണത്വരയ്ക്കും പുറമേ പാഠ്യേതര വിഷയങ്ങളില്‍ പ്രാഗല്ഭ്യവും വരുന്നതെങ്ങനെയെന്ന് ഊഹിക്കാമല്ലോ!

മറ്റു ചില സ്കൂളുകള്‍ പിന്തുടരുന്ന Everyday Mathematics പാഠ്യരൂപം പാര്‍ഷ്യല്‍ പ്രോഡക്ട്സ് രീതി എന്നും ലാറ്റിസ് രീതി എന്നും പേരായ രീതികള്‍ പിന്തുടരാന്‍ നിര്‍ദ്ദേശിക്കുന്നു.

പാര്‍ഷ്യല്‍ പ്രോഡക്ട്സ് രീതി നമുക്കു പരിചിതമായ സാധാരണ രീതിയുമായി വളരെ സാമ്യമുള്ളതാണ്. ഈ രീതിയില്‍ സംഖ്യകളുടെ സ്ഥാനക്രമം കുട്ടികള്‍ക്ക് വ്യക്തമാക്കിക്കൊടുക്കുന്നുണ്ട്. ചിത്രം നോക്കുക. ഇവിടെയും സംഖ്യകള്‍ വലുതാവുമ്പോഴുണ്ടാകുന്ന പ്രശ്നങ്ങളെക്കുറിച്ച് ചിന്തിക്കുക.


ചിത്രം: പാര്‍ഷ്യല്‍ പ്രോഡക്ട്സ് രീതി

Everyday Mathematics നിഷ്കര്‍ഷിക്കുന്ന ലാറ്റിസ് രീതി വളരെ രസാവഹമാണ്. ഗുണിക്കേണ്ടുന്ന സംഖ്യകള്‍ മുകളിലും വലതും ആകത്തക്ക വിധം ഒരു ഗ്രിഡ് ഉണ്ടാക്കുകയാണ് ആദ്യപടി. രണ്ടു അക്കങ്ങള്‍ ചേര്‍ന്നു വരുന്നയിടം രണ്ടായി പകുത്ത് (ചിത്രം കാണുക) അവിടെ രണ്ടു പകുതിയിലും കൂടി ആ സംഖ്യകളുടെ ഗുണനഫലം എഴുതിവയ്ക്കുക. ഗുണനഫലം ഒരക്ക സംഖ്യയാണെങ്കില്‍ ഗുണനഫലത്തിന്‍റെ ആദ്യ അക്കമായി 0 ഉപയോഗിക്കാം. ഇങ്ങനെ ഓരോ അക്കങ്ങളുടെ ഗുണനഫലവും അതാതു ഗ്രിഡുകളില്‍ എഴുതുക. ഇങ്ങനെ ചെയ്ത ശേഷം, ഡയഗണല്‍ ആയി വരുന്ന അക്കങ്ങളുടെ തുക കണ്ടു പിടിക്കുക. ഇതില്‍ നിന്നും സംഖ്യകളുടെ ഗുണനഫലത്തിലെത്തുന്ന വിധം താഴെ കാണിച്ചിരുക്കുന്നു.


ചിത്രം: ലാറ്റിസ് രീതി

കണക്കു പരീക്ഷയില്‍ രണ്ടു സംഖ്യകളുടെ ഗുണനഫലം കാണേണ്ടിവരുമ്പോള്‍ ലാറ്റിസ് രീതി മാത്രമറിയുന്നവര്‍ സമയം പോകുന്നത് അറിയുകയേയില്ല.

ഇങ്ങനെയാണെങ്കിലും എനിക്ക് വളരെ പ്രിയങ്കരമായ പെസന്‍റ് രീതി സ്കൂളുകളില്‍ പഠിപ്പിക്കുന്നതായി കാണുന്നില്ല. ആദ്യ വരിയില്‍ ഗുണിക്കപ്പെടേണ്ട രണ്ടു സംഖ്യകള്‍ നിരത്തിയെഴുതുക. രണ്ടാം വരിയില്‍, ആദ്യ സംഖ്യയുടെ താഴെ ആദ്യ സംഖ്യയെ രണ്ടു കൊണ്ട് ഹരിച്ച ഫലം (ശിഷ്ടം ഉപേക്ഷിക്കാം) എഴുതുക. രണ്ടാം സംഖ്യയ്ക്കു താഴെ, രണ്ടാം സംഖ്യയുടെ ഇരട്ടി എഴുതുക. വരിയിലെ ആദ്യസംഖ്യ ഒന്ന് ആകുന്നതു വരെ ഈ പ്രക്രിയ തുടരുക. ഇനി, ഓരോ വരിയിലെയും ആദ്യ സംഖ്യ നോക്കുക. ഈ സംഖ്യ ഇരട്ട സംഖ്യയാണെങ്കില്‍ ആ വരിയിലെ രണ്ടാം സംഖ്യ വെട്ടിക്കളയുക. ഇങ്ങനെ ആദ്യ കോളത്തിലെ ഇരട്ടസംഖ്യകള്‍ക്കു നേരേ രണ്ടാം കോളത്തിലെഴുതിയിരിക്കുന്ന സംഖ്യകള്‍ വെട്ടി മാറ്റിയ ശേഷം, രണ്ടാം കോളത്തില്‍ ബാക്കിയാവുന്ന സംഖ്യകളുടെ തുകയായിരിക്കും ആ സംഖ്യകളുടെ ഗുണനഫലം.


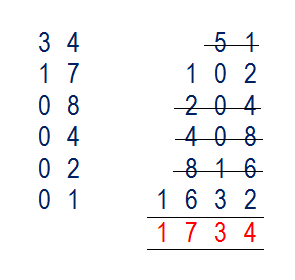
ചിത്രം: പെസന്‍റ് രീതി

ഗുണനവും ഹരണവുമെല്ലാം പഠിക്കുന്നതിനൊപ്പം കുട്ടികളുടെ ശാസ്ത്രാഭിവാഞ്ഛ വര്‍ധിപ്പിക്കുന്നത് നല്ലതാണെന്നതിന് ആര്‍ക്കും രണ്ടഭിപ്രായമില്ല. എന്നാല്‍ പഠനം ലാറ്റിസ് രീതിയില്‍ മാത്രമാവുകയും ദൈനംദിന ജീവിതത്തിലെ ചെറിയ കണക്കു കൂട്ടലുകള്‍ക്ക് ഈ രീതി അഭികാമ്യമല്ലാതാവുകയും ചെയ്യുമ്പോഴാണ് കുട്ടികള്‍ക്കൊപ്പം രക്ഷിതാക്കളും അഭിനവ പഠന രീതികളോട് പുറം തിരിഞ്ഞു നില്‍ക്കുന്നത്. സ്കൂളുകളില്‍ സാധാരണ രീതി നിര്‍ബന്ധമായും പഠിപ്പിക്കണമെന്നും മറ്റു രീതികള്‍ കൂടുതല്‍ താല്പര്യമുള്ള വന്‍‍പുലികള്‍ വിഹരിക്കേണ്ടുന്ന ഘോരവിപിനങ്ങളാക്കുന്നതില്‍ തങ്ങള്‍ക്കെതിര്‍പ്പില്ലെന്നുമാണ് ഈ ‘മൂരാച്ചി’കളുടെ വാദം. അതില്‍ കഴമ്പുണ്ടെന്ന് സമ്മതിക്കാതെ വയ്യ.

പുലിവേട്ട

പുപ്പുലിയായ ജ്യോതി എഴുതിയ കിം ലേഖനം വായിച്ച ശേഷമാണ് ഞാന്‍ പുലി വേട്ടയ്ക്കിറങ്ങിയത്. സാമാന്യം തരക്കേടില്ലാത്ത വേട്ടയായിരുന്നു. പത്തമ്പത് വമ്പന്മാരെ കിട്ടി. ഉണ്ട തീര്‍ന്നു പോയതുകൊണ്ടു മാത്രം അമ്പതില്‍ ഒതുക്കിയതാണ്. പിന്നെയാണോര്‍ത്തത് അങ്ങനെ ചെയ്തത് നന്നായെന്ന്. വെടിവച്ചിട്ട പുലികളെയെല്ലാം സൂക്ഷിച്ചുവയ്ക്കാനുള്ള കോപ്പ് എന്‍റെ കയ്യിലില്ല. മഴ നനഞ്ഞാല്‍ കുളമാകും. സീയാറ്റിലിലാണെങ്കില്‍ ഒരാഴ്ചയായി നിര്‍ത്താതെ മഞ്ഞു വീഴ്ചയും. എന്തു ചെയ്യും എന്നാലോചിച്ച് ഏ. ആറിനെ സമീപിച്ചു. നല്ല കാര്യ വിവരമുള്ള ആളാണ്, അദ്ദേഹം ഒരു വഴികാണിച്ചു തരാതിരിക്കില്ല. തെറ്റിയില്ല. ഓച്ഛാനിച്ചു നിന്ന എന്നെ നോക്കി അദ്ദേഹം പറഞ്ഞു:

“ശംഭുനടനം!”
“എന്തോ?” ഞാന്‍ ചോദിച്ചു.
“ജകാരസനഭത്തൊടു ജകാരസനഭം ലഘുഗുരുക്കളിഹ ശംഭുനടനം” അല്പം നീരസം കലര്‍ന്ന മറുപടി.

എനിക്ക് സമാധാനമായി. ഞാന്‍ തിരിഞ്ഞോടി. വീര്യമുള്ള മദ്യം മോന്തിയിട്ട് കയ്യാഫാസിനെപ്പോലെ ഞാന്‍ അലറി:

“എനിക്ക് തൃപ്തിയായി! ആ പുലിക്കൂട്ടങ്ങളെ ഞാന്‍ തറച്ചു! എന്‍റെ ശത്രുവിനെയും. ഈ മദ്യം എന്‍റെ സന്തോഷം കൂട്ടും!”

കാലാവസ്ഥയില്‍ എന്തോ മാറ്റം പോലെ. പട്ടാപ്പകല്‍ സൂര്യന്‍ മറയുന്നു. കൊടുങ്കാറ്റടിക്കുന്നു. ഏയ്, തോന്നിയതാവണം. അല്ല, ഇവിടെ ഇതൊക്കെ പതിവുള്ളതല്ലേ?

പുലിക്കൂട്ടങ്ങളെ വാരിയടുക്കി. മൂന്നു നിര കഴിഞ്ഞപ്പോള്‍ ആകെ തളര്‍ന്നു. മദ്യം മനുഷ്യനെ ശക്തനാക്കില്ല. അവന്‍റെ ദൌര്‍ബല്യത്തെ മറച്ചു പിടിക്കുകയേയുള്ളൂ. പുലികള്‍ ഇനിയും നിരന്നു കിടക്കുന്നു. എന്നു മാത്രമോ, തീര്‍ച്ചയായും കളയാന്‍ വയ്യാത്ത ചില വന്‍ പുലികള്‍ അറയ്ക്കുള്ളില്‍ കൊള്ളുന്നുമില്ല.

“നീ മദ്യപിച്ചിട്ടുണ്ടോ?”
നടുവ് പരമാവധി വളച്ചുകൊണ്ട് ബോധിപ്പിച്ചു: “കാലിക്കുപ്പിയില്‍ അല്പം വെള്ളം കലക്കി മണപ്പിച്ചു. അത്രേയുണ്ടായിട്ടുള്ളൂ. മാടന്‍ തമ്പുരാനാണെ...” “നിറുത്ത്!”

ഞാന്‍ നിറുത്തി. കള്ളയാണയിടാതെ രക്ഷപ്പെട്ടു. സുകൃതം.

“പുലികള്‍ പലതും പുറത്തായി, അല്ലേ?”
“അതെ, പ്രഭോ...”
“എട്ടുഭകാരമിരണ്ടുഗുരുക്കളുമായ് വരുകില്‍ കരുതീടതു ചന്ദനസാരം”
“വീണ്ടും ഇരുപത്താറ്?”
“ഇരുപത്താറിലധികമായാല്‍ ദണ്ഡകമാവും. മണത്തതിന്‍റെ വിഷമിറങ്ങും മുമ്പ് ശ്രമിച്ചു നോക്ക്.”

ശ്രമിച്ചു. എന്നിട്ടും പല പുലികളും പുറത്ത്.

ആദി, യതുല്യ, യുമേഷു, കുമാറു, നിഷാദു, വിശാല, ദിവാ, സിബു, ദില്‍ബനു, മിഞ്ചീം
ബിന്ദു, സു, ഡാലി, യമുല്ലയുമങ്ങനെ, ബെന്നി, മൊഴീ, മിടിവാള, രവിന്ദതു, സാക്ഷീ,
ലാപുട, വിശ്വ, മനൂ, കുറുമാ, നനിലും, ശനിയന്‍, പെരിയോന്‍, ഷിജു, ദേവ‍, മനു, ശ്രീ,
ജ്യോതി, കരിത്തലയന്‍, നള, നെന്നിവരൊക്കെ ബുലോഗ വനത്തിലെ പുപ്പുലികള്‍ താന്‍!

പുലികള്‍ക്ക് പേരിടുമ്പോള്‍ ആലോചിക്കണമായിരുന്നു. ഈ രക്തത്തില്‍ എനിക്ക് പങ്കില്ല.

പേരിടാനും പണം

What's in a name? that which we call a rose
By any other name would smell as sweet.

ഒരു പേരിലെന്തിരിക്കുന്നു? ഷേക്സ്പിയര്‍ ചോദിച്ച ചോദ്യം തന്നെ.

ഭാവി മുഴുവന്‍ പേരിലാണിരിക്കുന്നതെന്ന് കൈപ്പള്ളിയും ഉമേഷും ആവര്‍ത്തിച്ചു പറഞ്ഞിട്ടും ബോധ്യമാവാത്തവരുണ്ടോ? നിങ്ങളെ രക്ഷിക്കാന്‍ എനിക്കാവില്ല മക്കളേ, മടങ്ങിപ്പോ...

അതുശരി, അപ്പോള്‍ മടങ്ങാന്‍ തന്നെ തീരുമാനിച്ചല്ലേ? നാലാള് പറഞ്ഞാലേ വിശ്വസിക്കുകയുള്ളൂ എന്ന വാശി നല്ലതിനു തന്നെ. എന്നാലിതാ നാലാമനായി ഞാന്‍ അവതരിക്കുന്നു.

കുട്ടികളുടെ പേരിനെക്കുറിച്ചല്ല ഞാന്‍ പറയാന്‍ പോകുന്നത്. ചില ചില്ലറ ചരക്കുകളുടെ അഥവാ പ്രോഡക്റ്റുകളുടെയും കമ്പനികളുടെയും പേരിനെക്കുറിച്ചാണ്. (ചില സംസ്കാരങ്ങളില്‍ ചരക്ക്, പ്രോഡക്റ്റ് എന്നിവ ഭാരമേറിയ നാനാര്‍ഥങ്ങള്‍ വഹിക്കുന്ന വാക്കുകളാണ്. തുടര്‍ന്ന് വായിക്കുന്നതിനുമുമ്പ് മലയാള സംസ്കാരത്തിന്‍റെ മുഖം‍മൂടി എടുത്തണിയാന്‍ അപേക്ഷ.)

നമുക്ക് ഒരു ചോദ്യോത്തര പരിപാടിയോടെ തുടങ്ങാം. എന്തുചെയ്യാന്‍, റ്റി. വി. കണ്ടുകണ്ട് ചോദ്യോത്തര മഴ ഒരു വീക്നെസ് ആയിപ്പോയി. ഞാന്‍ ചില വാക്കുകള്‍ പറയും. നിങ്ങളുടെ മനസ്സിലേയ്ക്ക് ആദ്യം കടന്നുവരുന്നത് എന്താണെന്ന് പറയണം.

കണ്ണന്‍ ദേവന്‍
അനിക്സ്പ്രേ
പുളിമൂട്ടില്‍
റീഗല്‍
ഇദയം
സെയ്ന്‍റ് ജോര്‍ജ്

(വാക്കുകള്‍ സ്പോണ്‍സര്‍ ചെയ്തത്: ഗുരുകുലം പാഠശാല, പോര്‍ട്ട്ലാന്‍ഡ്, അമേരിക്ക. നിങ്ങളുടെ കുട്ടികളെ ഉത്തരവാദിത്തത്തോടെ ‘കൈകാര്യം’ ചെയ്യുന്ന, നൂറു ശതമാനം വിജയം ഉറപ്പുതരുന്ന, അമേരിക്കയിലെ ഏക സ്ഥാപനം. അരാഷ്ടീയതയുടെ കൂത്തരങ്ങാണ് ഈ വിദ്യാലയം എന്ന വാദം പ്രിന്‍സിപ്പല്‍ നിഷേധിച്ചിട്ടുണ്ട്.)

ചുരുക്കത്തില്‍, ഈ പേരുകള്‍ റേഡിയോ/റ്റി. വി. പരസ്യങ്ങള്‍ വഴി നമ്മുടെ മനസ്സില്‍ ചിരപ്രതിഷ്ഠ നേടിയിരിക്കുന്നു എന്നു മനസ്സിലായില്ലേ?

കാര്യങ്ങളുടെ കിടപ്പ് ഇന്നത്തെയത്ര വഷളാവുന്നതിനു മുമ്പ് സ്വന്തം കമ്പനികള്‍ക്കും ഉല്പന്നങ്ങള്‍ക്കും പേരിട്ടവര്‍ ഭാഗ്യവാന്മാര്‍. ഹോണ്ട, റ്റൊയോറ്റ, ഹണിവെല്‍, ഡെല്‍ എന്നിവര്‍ അധികം ആലോചിക്കാതെ സ്ഥാപകരുടെ പേരുതന്നെ കമ്പനികള്‍ക്കു നല്‍കുകയായിരുന്നു. സന്തോഷ് ഹെയര്‍ ഓയില്‍ ഈ വിഭാഗത്തില്‍ വരുമെന്ന് തോന്നുന്നു. AVT-തേയില ഉടമയുടെ പേരിന്‍റെ ചുരുക്കപ്പേരാണെന്നാണ് അറിവ്.

അഡോബി (Adobe) എന്നത് ആ കമ്പനിയുടെ സ്ഥാപകരുടെ വീടിന്‍റെ പിന്നാമ്പുറത്തുകൂടി ഒഴുകിയിരുന്ന ഒരു ചെറു തോടിന്‍റെ പേരാണ്. ആമസോണ്‍ എന്താണെന്നും എവിടെയാണെന്നും നമുക്കെല്ലാമറിയാം. നോകിയ എന്നത് ഫിന്‍ലാന്‍ഡിലെ ഒരു ചെറിയ പട്ടണമാണ്. പെരിയാര്‍ പുട്ടുപൊടിയും മലബാര്‍ ഗോള്‍ഡും കൊല്ലം സുപ്രീം ഗോള്‍ഡ് കവറിംഗും ഈ ഗണത്തില്‍ പെടുത്താവുന്നവ തന്നെ.

ചില ഏഷ്യന്‍ കമ്പനികളാവട്ടെ, പേരിടുന്നതില്‍ മറ്റൊരു മാനദണ്ഡം സ്വീകരിച്ചു. Daewoo എന്നാല്‍ കൊറിയന്‍ ഭാഷയില്‍ ‘മഹത്തായ പ്രപഞ്ചം’ എന്നാണര്‍ഥം (കൊറിയയില്‍ നിന്നുള്ള ബ്ലോഗര്‍മാരുടെ തല്ലു കിട്ടുമോ എന്തോ!). ഹിറ്റാചി, ‘സൂര്യോദയം’ എന്നര്‍ഥമുള്ള ഒരു പുരാതന സ്ഥലമത്രേ. സാംസങ് എന്ന വാക്കിന്‍റെ അര്‍ഥം മൂന്ന് നക്ഷത്രങ്ങള്‍ എന്നാണ്. (ദേ, വീണ്ടും കൊറിയന്‍!)

വളരെ ‘കാര്യമാത്ര പ്രസക്തരായവരും’ ഇക്കൂട്ടത്തിലുണ്ട്, നമ്മുടെ SBT, SBI എന്നിവരെപ്പോലെ. BMW എന്നാല്‍ Bayerische Motoren Werke എന്നതിന്‍റെ ചുരുക്കപ്പേര് മാത്രം. അതായത്, Bavarian Motor Factories. മറ്റൊരു വമ്പനാണ് AT&T: American Telephone and Telegraph.

ധനലക്ഷ്മി ബാങ്കിന് ആ പേര് ചേരുന്നതാണ്. ഗ്രീക്ക് പുരാണത്തിലെ വിജയത്തിന്‍റെ ദേവതയാണ് നൈക്കി (Nike). വിജയികള്‍ അണിയുന്നത് (അണിയേണ്ടത്) എന്ന നിലയ്ക്ക് നൈക്കി വളരെ യോജിച്ച പേരാണ്. പുറത്തുനിന്നു നോക്കിയാല്‍ ചെറിയ കടയാണെങ്കിലും അതിവിശാലമായ ഷോറൂമായ അയ്യപ്പാസിന് പണം വാരുന്ന ദേവനുമായി ബന്ധമുണ്ടോ എന്ന് വ്യക്തമല്ല. മാരുതിയ്ക്കും അദിതിയ്ക്കും ആ പേരുകള്‍ കിട്ടിയത് എവിടെ നിന്നാണെന്ന് ഊഹിക്കാമല്ലോ.

ഇനിയും ചിലരുണ്ട്. പേരുണ്ടാക്കുന്നതില്‍ ഭാവന കലര്‍ത്തിയവര്‍. ഒന്നിനു ശേഷം 100 പൂജ്യം വരുന്ന സംഖ്യയ്ക്ക് ഗൂഗോള്‍ എന്നാണ് പേര്. അനന്തമായ വിവരം അടുക്കിയവതരിപ്പിക്കാനുള്ള ശ്രമവുമായിത്തുടങ്ങിയ കമ്പനിയായ ഗൂഗിളിന് മനഃപൂര്‍വം തെറ്റായുച്ചരിച്ചുണ്ടാക്കിയ പേര് നന്നായി ചേരുന്നു. (സിബൂ, തല്ലരുത്‌, ഒന്നു വിരട്ടി വിട്ടാല്‍ മതി!)

ഭാവനയില്‍ ഒരു പടി കൂടി കടന്നവരാണ് CD/DVD-കള്‍ എഴുതാന്‍ ഉപയോഗിക്കുന്ന സോഫ്റ്റ്‍വെയര്‍ ആയ നീറോ. Nero burning Rome എന്ന വാചകത്തെ അവര്‍ ഇങ്ങനെയാണ് ‘മാറ്റി’യെഴുതിയത്: Nero Burning ROM.

എന്നാലിന്നോ? പരസ്യവാചകങ്ങളോളമോ അതിനേക്കാളുമോ പ്രധാനമാണ് പരസ്യം ചെയ്യപ്പെടുന്ന സാധനത്തിന്‍റെ പേര് എന്നായിരിക്കുന്നു.

കുട്ടികളുണ്ടായിട്ടുള്ളവര്‍ക്കറിയാം, കുഞ്ഞിന്‍റെ പേര് തീരുമാനിക്കാന്‍ മാതാപിതാക്കള്‍ അനുഭവിക്കുന്ന പെടാപ്പാട്. പത്തുനൂറ് പേരുകളില്‍ നിന്ന് ചുരുക്കിച്ചുരുക്കി രണ്ടോ നാലോ പേരിലെത്തിക്കാനുള്ള പാട്, പിന്നെ അതില്‍ നിന്ന് ഒരെണ്ണം തെരഞ്ഞെടുക്കാനുള്ള പാട്... അവസാനം ഭാര്യയ്ക്കും ഭര്‍ത്താവിനും ഇഷ്ടപ്പെട്ട പേര് തീരുമാനിച്ചു കഴിയുമ്പോള്‍ അമ്മയും അമ്മായിയമ്മയും ഒരേ സ്വരത്തില്‍ ‘അയ്യേ!’ എന്നു പറയുന്നത് കേള്‍ക്കേണ്ടി വരുന്നത് ഒന്നാലോചിച്ചു നോക്കൂ. (ആറ്റുനോറ്റുണ്ടായ ഓപറേറ്റിംഗ് സിസ്റ്റത്തിന് പേരിട്ടത് വിസ്ത എന്നാണ് എന്ന് ആദ്യമായി കേട്ടപ്പോള്‍ തോന്നിയ പോലൊരു ഫീലിംഗ്.)

പേരിടാന്‍ വന്‍‍തുക വാങ്ങുന്ന സ്ഥാപനങ്ങള്‍ നിലവിലുണ്ട്. മൈക്രോസോഫ്റ്റ് ഈയിടെ പുറത്തിറക്കിയ പോര്‍ട്ടബിള്‍ മീഡിയ പ്ലെയറിന് സൂണ്‍ (Zune) എന്ന പേര് കണ്ടെത്തിയത് ലെക്സിക്കന്‍ ബ്രാന്‍ഡിംഗ് എന്ന സ്ഥാപനമാണ്. ഒരു പേര് നിര്‍ദ്ദേശിക്കുന്നതിന് ലെക്സിക്കന്‍ ബ്രാന്‍ഡിംഗ് വാങ്ങുന്ന കുറഞ്ഞ തുക 150,000 ഡോളര്‍ ആണത്രേ. നൂറോളം ഭാഷകള്‍ പരിശോധിച്ച് ‘വലിയ പ്രശ്നമില്ലാത്ത’ സൂണ്‍ എന്ന പേര് നിര്‍ദ്ദേശിക്കാന്‍ ഭീമമായ തുകയാവണം ലെക്സിക്കന്‍ ബ്രാന്‍ഡിംഗ് ഈടാക്കിയിട്ടുള്ളത്.

ലെക്സിക്കന്‍ ബ്രാന്‍ഡിംഗ് ചില്ലറക്കാരല്ല. പെന്‍റിയം, ബ്ലാക്ബെറി തുടങ്ങി ഇന്ന് പരസ്യ ലോകത്ത് നിറഞ്ഞു നില്‍ക്കുന്ന പല ബ്രാന്‍ഡ് പേരുകളുടേയും സ്രഷ്ടാക്കളാണവര്‍. സൂണ്‍ എന്ന പേര് കണ്ടെത്താന്‍ മുപ്പത്തൊമ്പത് രാജ്യങ്ങളിലുള്ള അറുപതോളം ഭാഷാശാസ്ത്രജ്ഞരുടെ സഹായം ലെക്സിക്കന്‍ ബ്രാന്‍ഡിംഗ് ഉപയോഗപ്പെടുത്തി. ഏഴില്‍ താഴെമാത്രം ഇംഗ്ലീഷ് അക്ഷരങ്ങളുള്ള മൂവയിരത്തി അഞ്ഞൂറ് വാക്കുകള്‍ അവര്‍ പരിഗണിച്ചു. കൂടുതല്‍ വിവരങ്ങള്‍ ഇവിടെയുണ്ട്.

സൂണ്‍ എന്ന പേരിനു പിന്നിലെ മനഃശാസ്ത്രം ചോദിച്ചവരോട് ലെക്സിക്കന്‍ ബ്രാന്‍ഡിംഗ് സ്ഥാപകന്‍ ഡേവിഡ് പ്ലാസെക് പറഞ്ഞതിങ്ങനെ:

ഇംഗ്ലീഷ് ഭാഷയിലെ ജീവസ്സുറ്റതും ഓജസ്സുള്ളതുമായ ശബ്ദമാണ് Z (അമേരിക്കക്കാര്‍ Z-നെ ‘സ്സീ’ എന്നാണ് ഉച്ചരിക്കുന്നത് zebra-യിലെ ze ഉച്ചരിക്കുന്നതു പോലെ). K, C, G എന്നിവയ്ക്കുള്ളതുപോലുള്ള വിശ്വാസ്യതയുടെ മാസ്മരിക പ്രഭാവം Z-യ്ക്കുമുണ്ട്.

...

The buzz of the sound "z" makes it one of the most energetic in the language. Lexicon's studies of sound symbolism, conducted with hundreds of people in a variety of languages, have shown that word-initial "z" scores very high for communicating attributes like "lively," "daring," and "fast."

The letter z's current popularity in respellings like "boyz" and "antz" lends a youthful irreverence. Even though it isn't obviously derived from any real word, Zune could pass for a casual abbreviation, in the same way that 'zza stood in for pizza with some people 10 years or so ago.

അനതിവിദൂര ഭാവിയില്‍ നമ്മുടെ നാടും ഈ കച്ചവട തന്ത്രം നടപ്പിലാക്കിക്കൂടായ്കയില്ല. പുതിയ സം‍രംഭങ്ങളുമായി രംഗത്തേയ്ക്ക് വരുന്നവരാണ് ഇനി “ശക്തവും പ്രഭാപൂരവും ജീവസ്സുറ്റതും” ആയ പേരിന് പണമിറക്കേണ്ടി വരുന്നത്. കുട്ടികളുടെ പേരിടാനും ഇത്രത്തോളമോ ഇതിലുമധികമോ ശ്രദ്ധവയ്ക്കുന്ന (പണമിറക്കുന്ന) ഒരു കാലം വന്നേക്കും. നല്ല പേരുകള്‍ ഉണ്ടാക്കിയെടുക്കാനുള്ള വാസനയുണ്ടോ? അവസരങ്ങള്‍ നിങ്ങള്‍ക്കു മുന്നില്‍ തുറന്നു കിടക്കുന്നു!